JPS 算法概念基础

  • JPS（Jump Point Search，跳点搜索）算法是对 A* 算法的一种优化（附A* 算法）。在 A* 算法中，当前节点周围的所有可搜索邻居都会被加入到 OpenList 中。JPS 算法则在保持 A* 算法基本框架的基础上，采用了一种更为高效的策略来确定哪些点需要被加入到 OpenList 中。这种方法能够显著减少需要评估的节点数量，从而提高路径搜索的效率。

自然邻居

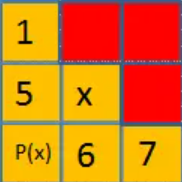
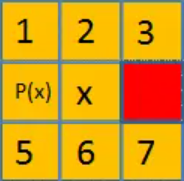
  • 自然邻居指的是在路径搜索过程中，某些节点的直接邻居是可以直接移动到达的节点，而不需要经过其他节点的中转。这些自然邻居是基于当前节点的移动方向和位置来确定的。如图所示，红色块是自然邻居（其中 p(x) 为父节点，x为当前节点）。

JPS 自然邻居 1 JPS 自然邻居 2

强迫邻居

  • 为了减少需要评估的节点数量，JPS 算法引入了强迫邻居的概念。强迫邻居指的是在路径搜索过程中，某些节点的直接邻居是必须被考虑的，因为它们是达到更远距离节点的必经之路。在 JPS 算法中，强迫邻居用于确保搜索过程不会错过任何可能的路径选择。
  • 强迫邻居的定义：当节点 x 的 8 个邻居中存在障碍，且节点 x 的父节点 p 经过节点 x 到达节点 n 的距离代价，总是小于不经过节点 x 到达节点 n 的任意路径的距离代价，则称节点 n 是节点 x 的强迫邻居。简单来讲，节点 x 是从节点 p 到节点 n 的最短路径的必经节点。
  • 我们先作一些定义：考虑节点 x 的邻居，节点 x 的父节点记为 p(x), 记经过 x 到达 n 的路径为 path1，不经过 x 到达 n 的路径为 path2

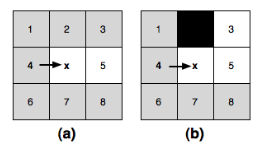
情况一：父子节点是直线关系

JPS 强迫邻居 1

  • 黑色节点：障碍; 4：父节点; x：子节点。针对图 b，从 4 到 3 的最短路径为：4 → x → 3，因此 3 是节点 x 的强迫邻居
  • 如果父子节点之间是直线关系，即父节点经过一次斜线运动可以直接到达子节点，我们不需要考虑存在 path2 小于等于 path1 的邻居。
  • 先考虑图（a）的情况，我们修剪除 n = 5 之外的所有邻居。以 n = 3 为例：
    • path1 = 4 → x → 3：路径长度为 $ 1 + \sqrt{2} $
    • path2 = 4 → 2 → 3：路径长度为 $ 1 + \sqrt{2} $
  • 这里path1 == path2，需要将该邻居修剪（拒绝加入 OpenList）
  • 因此，对于图（a），x 的下一步应该继续往 5 走，但是不将 5 加入 OpenList。
  • 再考虑图（b）带黑色障碍的情况。相比图（a），我们多了个 n = 3 的邻居无法被修剪。

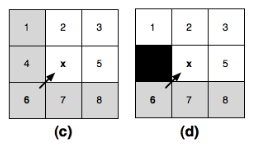
情况二：父子节点是斜线关系

JPS 强迫邻居 2

  • 黑色节点：障碍; 6：父节点; x：子节点。针对图 d，从 6 到 1 的最短路径为：6 → x → 1，因此 1 是节点 x 的强迫邻居
  • 当父子节点是斜线关系时，邻居的修剪规则和直线关系的情况类似，唯一的区别是，此时只修剪存在 path2 严格小于 path1 的邻居。因此，按照此规则，n = 2 和 n = 5 的情况不会被修剪。
  • 再考虑图（d）带黑色障碍的情况。相比图（c），我们多了个 n = 1 的邻居无法被修剪。

得到强迫邻居

  • 图（a）和图（c）不包含任何障碍，我们将应用直线或对角线修剪后的剩余节点（白色格子）称为 x 的自然节点。灰色格子则是 x 的非自然节点。而对于图（b）和图（d），包含障碍之后，各自有一个非自然节点（分别为 n = 3 和 n = 1）无法被修剪，这两个节点则被称为 x 的强迫邻居。

跳点

跳点的要求

  • 当节点 x 满足以下三个条件之一，则称节点 x 为跳点：
    1. 节点 x 是起始点或目标点
    2. 节点 x 至少有一个强迫邻居
    3. 如果节点 x 的父节点 p(x) 到节点 x 是对角线移动，且 x 可以通过水平或垂直方向的移动到达另一个跳点，则节点 x 也是跳点。

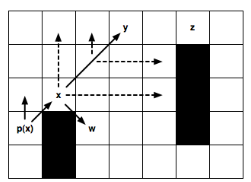
识别跳点的例子

JPS 跳点识别

  • 从 x 开始，水平和垂直方向都没有遇到跳点，因此沿着对角线行进。继续重复水平、垂直、对角线。直到到达节点 y。
  • 从节点 y 开始，水平移动 2 格，到达节点 z。节点 z 是跳点，且根据条件 3，节点 y 也是跳点。

算法流程

  • 有了跳点的概念之后，接下来我们就可以介绍 JPS 算法的具体流程：
    • 初始化：将起点加入到 OpenList 中。
    • 搜索跳点：
      1. 从 OpenList 中取出具有最小 f 值的节点作为当前节点（这部分和 A* 算法一样），并将其加入到 CloseList 中
      2. 搜寻当前节点的自然邻居和强迫邻居
      3. 遍历所有自然邻居和强迫邻居，根据邻居方向开始往水平 || 垂直 || 对角线方向搜索跳点。对角线方向的搜索需要先检查当前邻居是否有强迫邻居，如果有则将当前邻居加入到 OpenList 中，并停止当前方向的搜索。否则优先考虑水平分量，然后是垂直分量。如果找到跳点，则将该跳点加入到 OpenList 中，并停止当前方向的搜索。
    • 重复搜索：重复执行搜索跳点步骤，直到找到目标点或 OpenList 为空。
  • 下面是搜索挑点步骤中第二点（评估当前节点的邻居方向）和第三点（跳点）的代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/// <summary>
/// 评估当前节点的邻居方向
/// </summary>
/// <param name="nodeX">当前需要评估的节点的 X 坐标</param>
/// <param name="nodeY">当前需要评估的节点的 Y 坐标</param>
/// <param name="node">当前需要评估的节点</param>
/// <returns>需要探索的邻居方向偏移量列表(dx, dy)</returns>
private List<(int dx, int dy)> EvaluateNeighbor(int nodeX, int nodeY, JPSNode node)
{
    List<(int dx, int dy)> neighbors = new List<(int dx, int dy)>();

    // 如果是起点（没有父节点），返回所有 8 个可走方向
    if (node.father == null)
    {
        for (int i = 0; i < 8; i++)
        {
            int dx = m_Direction[i, 0];
            int dy = m_Direction[i, 1];
            if (IsWalkable(nodeX + dx, nodeY + dy)) neighbors.Add((dx, dy));
        }
        return neighbors;
    }

    // 计算移动方向
    (int nodeFatherX, int nodeFatherY) = WorldPositionToJPSPosition(node.father.position);
    int dxDir = Mathf.Clamp(nodeX - nodeFatherX, -1, 1);
    int dyDir = Mathf.Clamp(nodeY - nodeFatherY, -1, 1);

    // 辅助函数：防止穿墙判定
    bool CanMoveDiagonal(int cx, int cy, int dx, int dy)
    {
        // 目标必须可走
        if (!IsWalkable(cx + dx, cy + dy)) return false;
        // 防穿墙：水平或垂直方向至少有一个可走（宽松模式）
        // 若要严格模式（不能蹭墙角），改为 && 
        return IsWalkable(cx + dx, cy) || IsWalkable(cx, cy + dy);
    }

    // 1. 对角线移动
    if (dxDir != 0 && dyDir != 0)
    {
        // 自然邻居：前方，水平分量，垂直分量
        if (CanMoveDiagonal(nodeX, nodeY, dxDir, dyDir)) neighbors.Add((dxDir, dyDir));
        if (IsWalkable(nodeX + dxDir, nodeY)) neighbors.Add((dxDir, 0));
        if (IsWalkable(nodeX, nodeY + dyDir)) neighbors.Add((0, dyDir));

        // 强迫邻居 (Forced Neighbor)
        // 只有当反方向水平阻挡，且该方向的对角线可达时，该对角线是强制邻居
        if (!IsWalkable(nodeX - dxDir, nodeY) && CanMoveDiagonal(nodeX, nodeY, -dxDir, dyDir)) neighbors.Add((-dxDir, dyDir));
        
        // 只有当反方向垂直阻挡，且该方向的对角线可达时，该对角线是强制邻居
        if (!IsWalkable(nodeX, nodeY - dyDir) && CanMoveDiagonal(nodeX, nodeY, dxDir, -dyDir)) neighbors.Add((dxDir, -dyDir));
    }
    // 2. 直线移动
    else
    {
        if (dxDir != 0) // 水平移动
        {
            if (IsWalkable(nodeX + dxDir, nodeY))
            {
                neighbors.Add((dxDir, 0));
                // 检查上方强迫邻居
                if (!IsWalkable(nodeX, nodeY + 1) && CanMoveDiagonal(nodeX, nodeY, dxDir, 1)) neighbors.Add((dxDir, 1));
                // 检查下方强迫邻居
                if (!IsWalkable(nodeX, nodeY - 1) && CanMoveDiagonal(nodeX, nodeY, dxDir, -1)) neighbors.Add((dxDir, -1));
            }
        }
        else // 垂直移动
        {
            if (IsWalkable(nodeX, nodeY + dyDir))
            {
                neighbors.Add((0, dyDir));
                // 检查右侧强迫邻居
                if (!IsWalkable(nodeX + 1, nodeY) && CanMoveDiagonal(nodeX, nodeY, 1, dyDir)) neighbors.Add((1, dyDir));
                // 检查左侧强迫邻居
                if (!IsWalkable(nodeX - 1, nodeY) && CanMoveDiagonal(nodeX, nodeY, -1, dyDir)) neighbors.Add((-1, dyDir));
            }
        }
    }

    return neighbors;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
/// <summary>
/// JPS 核心：跳跃函数
/// </summary>
/// <param name="cx">当前位置 x</param>
/// <param name="cy">当前位置 y</param>
/// <param name="dx">方向 x</param>
/// <param name="dy">方向 y</param>
/// <param name="endNode">终点</param>
/// <returns>找到的跳点或 null</returns>
private JPSNode SearchJumpNode(int cx, int cy, int dx, int dy, JPSNode endNode)
{
    while (true)
    {
        // --- 1. 移动前置检查（防穿墙逻辑） ---
        // 如果是对角线移动，必须确保没有“卡墙角”
        if (dx != 0 && dy != 0)
        {
            // 规则：前往 (cx+dx, cy+dy) 时，(cx+dx, cy) 和 (cx, cy+dy) 不能同时阻挡（宽松）
            // 或者：只要有一个阻挡就不能走（严格）
            // 这里使用相对宽松的规则：只要有一个方向是通的就可以走，但如果都堵住了就不能走
            // 同时也隐含检查了目标点 (cx+dx, cy+dy) 是否可走
            
            // 检查目标点是否可走
            if (!IsWalkable(cx + dx, cy + dy)) return null;

            // 检查墙角阻挡 (防穿墙)
            // 如果右边是墙 且 下边是墙，则不能向右下穿过
            if (!IsWalkable(cx + dx, cy) && !IsWalkable(cx, cy + dy)) return null;
            
            // 如果需要更严格的物理碰撞（只要蹭到墙角就不能走），使用下面这行：
            // if (!IsWalkable(cx + dx, cy) || !IsWalkable(cx, cy + dy)) return null;
        }
        else
        {
            // 直线移动，仅检查目标点
            if (!IsWalkable(cx + dx, cy + dy)) return null;
        }

        // --- 2. 执行移动 ---
        cx += dx;
        cy += dy;

        JPSNode currentNode = m_Map[cx, cy];

        // --- 3. 检查是否到达终点 ---
        if (currentNode == endNode) return currentNode;

        // --- 4. 检查强制邻居 (Forced Neighbor) ---
        
        // 4.1 对角线移动 (dx != 0, dy != 0)
        if (dx != 0 && dy != 0)
        {
            // 检查逻辑：
            // 如果反方向水平受阻 (x-dx, y)，但该受阻点的“前方” (x-dx, y+dy) 可走 -> 发现强制邻居
            bool forcedH = !IsWalkable(cx - dx, cy) && IsWalkable(cx - dx, cy + dy);
            // 如果反方向垂直受阻 (x, y-dy)，但该受阻点的“前方” (x+dx, y-dy) 可走 -> 发现强制邻居
            bool forcedV = !IsWalkable(cx, cy - dy) && IsWalkable(cx + dx, cy - dy);

            if (forcedH || forcedV)
            {
                return currentNode;
            }

            // --- 递归检查水平和垂直分量 ---
            // 只有当当前点本身是合法的位置时，才有资格去检查分量
            // (dx, 0) 和 (0, dy) 的检查不会产生无限递归，深度为 1
            if (SearchJumpNode(cx, cy, dx, 0, endNode) != null || 
                SearchJumpNode(cx, cy, 0, dy, endNode) != null)
            {
                return currentNode;
            }
        }
        // 4.2 直线移动
        else
        {
            // 水平移动 (dx != 0)
            if (dx != 0)
            {
                // 上方有墙 且 dx 方向的上方可走 || 下方有墙 且 dx 方向的下方可走
                if ((!IsWalkable(cx, cy + 1) && IsWalkable(cx + dx, cy + 1)) ||
                    (!IsWalkable(cx, cy - 1) && IsWalkable(cx + dx, cy - 1)))
                {
                    return currentNode;
                }
            }
            // 垂直移动 (dy != 0)
            else
            {
                // 右侧有墙 且 右侧 dy 方向可走 || 左侧有墙 且 左侧 dy 方向可走
                if ((!IsWalkable(cx + 1, cy) && IsWalkable(cx + 1, cy + dy)) ||
                    (!IsWalkable(cx - 1, cy) && IsWalkable(cx - 1, cy + dy)))
                {
                    return currentNode;
                }
            }
        }
    }
}

JPS 相比 A* 算法的优势

  • 效率提升：JPS算法通过只扩展关键的跳点（即路径改变方向的点），而不是每个可能的节点，从而显著减少了 OpenList 中节点的数量，提高了搜索效率。
  • 内存使用降低：由于 OpenList 中节点数量的减少，JPS算法在内存使用上也更加高效。
  • 适用于大规模地图：JPS 算法在大规模地图上的表现尤为出色，因为它能够快速地跳过大片可行走区域，而不需要逐个节点地进行评估。

JPS 相比 A* 算法的劣势